数据结构作业——绳子与重物

发表于 分类于 阅读次数：

绳子与重物
时间限制: 400 ms
内存限制: 64 MB

有N条绳子编号 0 至 N - 1，每条绳子后面栓了一个重物重量为Wi，绳子的最大负重为Ci。每条绳子或挂在别的绳子下或直接挂在钩子上（编号-1）。如果绳子下所有重物的重量大于绳子的最大负重就会断掉（等于不会断）。依次给出每条绳子的负重Ci、重物的重量Wi以及绳子会挂在之前的哪条绳子的下面，问最多挂多少个绳子而不会出现绳子断掉的情况。

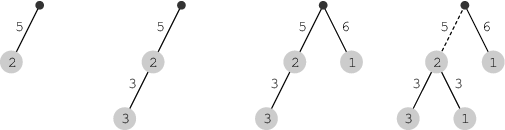
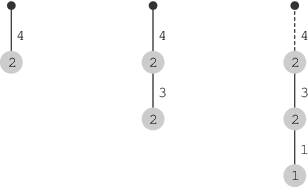
例如下图：

5, 2, -1
3, 3, 0
6, 1, -1
3, 1, 0
3, 2, 3

挂到第4个时会有绳子断掉，所以输出3。

输入格式：
第1行：1个数N，表示绳子的数量(1 <= N <= 50000)。
第2 - N+1行：每行3个数，Ci, Wi, Pi。Ci表示最大负重，Wi表示重物的重量，Pi表示挂在哪个绳子上，如果直接挂在钩子上则Pi = -1（1 <= Ci <= 10^9，1 <= Wi <= 10^9，-1 <= Pi <= N - 2)。

输出格式：
输出1个数，最多挂到第几个绳子，不会出现绳子断掉的情况。

输入样例:

1
2
3
4
5
6
5
5 2 -1
3 3 0
6 1 -1
3 1 0
3 2 3

输出样例:

1
3

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <stdio.h>
#include <stdlib.h>

struct node
{
    int c, w, p, fa;
    long long sum;
};

struct node *a;

/* 路径压缩的递归实现，大规模数据可能造成栈溢出
int find(int n)
{
    if(a[n].fa != n)
        a[n].fa = find(a[n].fa);
    return a[n].fa;
}
*/

// 路径压缩的非递归实现
int find(int n)
{
    int root = n, curr = n, temp;
    while(a[root].fa != root)
        root = a[root].fa;
    while(curr != root)
    {
        temp = a[curr].fa;
        a[curr].fa = root;
        curr = temp;
    }
    return root;
}

int main()
{
    int n, ans;
    scanf("%d", &n);

    a = (struct node *)malloc(sizeof(struct node) * n);
    for(int i = 0; i < n; ++i)
    {
        scanf("%d%d%d", &a[i].c, &a[i].w, &a[i].p);
        a[i].fa = i;
        a[i].sum = a[i].w;
    }

    ans = n-1;
    for(int i = n-1; i >= 0; --i)
    {
        while(a[i].sum > a[i].c)
        {
            a[find(ans)].sum -= a[ans].w;
            ans--;
        }
        a[a[i].p].sum += a[i].sum;
        if(a[i].p > -1)
            a[i].fa = a[i].p;
    }

    printf("%d", ans+1);
    return 0;
}