摘要:汉诺塔问题如何解决?有何规律与方法?通过发现、研究、总结规律,探索出解决n个盘子汉诺塔问题的方法。
关键词:汉诺塔、递归
第一部分、问题的提出
汉诺(Hanoi)塔问题是源于法国数学家爱德华·卢卡斯编写的一个印度古老传说的益智玩具。其规则是:现有三根柱,即A柱、B柱与C柱,在A柱上从上往下按照从小到大的顺序摞着64片圆盘,要求在大盘不能在小盘之上、一次只能移动一个圆盘的前提下,把圆盘按大小顺序完全移动至C柱(如图1所示)。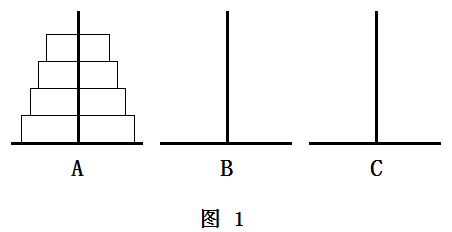
要想完成这个游戏,需要按怎样的步骤移动?至少需要多少步才能完成?怎样移动步数最少?一个个问题困扰着我,于是我对汉诺塔问题展开了探究。
第二部分、问题的探究
要想解决原题目中64个圆盘的汉诺塔问题,不妨先从简单的汉诺塔问题入手,再从特殊到一般,总结出n个盘子的规律。
经过一段时间的尝试,我发现1个盘子的汉诺塔问题只需一步即可解决,即A—>C;2个盘子的汉诺塔问题最少需要三步来解决,即A—>B,A—>C,B—>C;3个盘子的汉诺塔问题最少需要七步来解决,即A—>C,A—>B,C—>B,A—>C,B—>A,B—>C,A—>C。这三种简单情况之需经过简单的尝试即可解决,但从4个盘子开始,问题变得越来越复杂,经过屡次尝试我才找到了最少步数的解决方法:A—>C,A—>B,C—>B,A—>C,B—>A,B—>C,A—>C,共15步。
通过上面的四次尝试,我对于盘子数(n)与最少步数(S)列出下表:
| n/个 | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|
| S/步 | 1 | 3 | 7 | 15 | … |
根据表中数据,我做出大胆猜测:最少步数(S)与盘子数(n)成正相关,且S=2^n-1。
为了验证以上猜想的正确性,我开始寻找n=2、3、4时移动步骤的共性。若从原始条件出发没有头绪,不妨试试从结果出发。因为目的是把所有盘子移动到C柱,而又必须遵循大在下小在上的原则,那么就必须先把最大的盘子移动到C柱,再把次大的盘子移动到C柱,再把第三大的盘子移动到C柱,循环往复,直到最小的盘子也“抵达”C柱。
这个方法就好比大货车与小轿车发生车祸,轿车被压在货车下,一名行人被压在轿车之下。要想先救出被压在车底的人,就必须先把车一并抬起,移动到他处,再把人救出。
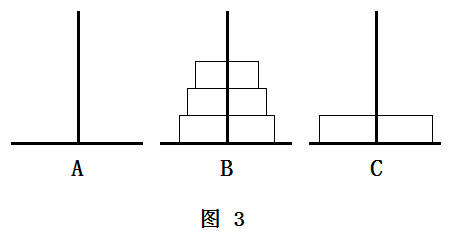
经过思考,我发现,不论2个、3个还是4个盘子,都是先想办法把A柱上除最后一个盘子以外的所有盘子移动到B柱上(如图2所示),这样就得以把A柱上剩下的最大的盘子移动至C柱(如图3所示);这时B柱上套着除最大盘外所有的盘子,B柱就好比一开始的A柱,A柱就变为空柱;把B柱上除最后一个盘子以外的所有盘子移动到A柱上(如图4所示),这样就得以把B柱上剩下的次大的盘子移动至C柱(如图5所示)……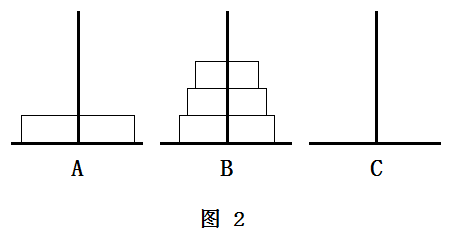
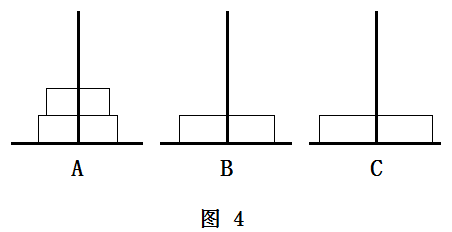
实践是检验真理的唯一标准,借助这个思路,我成功地解决了5个盘子的汉诺塔问题,步骤为:A—>C,A—>B,C—>B,A—>C,B—>A,B—>C,A—>C,A—>B,C—>B,C—>A,B—>A,C—>B,A—>C,A—>B,C—>B,A—>C,B—>A,B—>C,A—>C,B—>A,C—>B,C—>A,B—>A,B—>C,A—>C,A—>B,C—>B,A—>C,B—>A,B—>C,A—>C,共计31步,这也成功地验证了我对于步数与盘子数之间关系:S=2^n-1的猜想。
综上所述,我总结出了解决n个盘子的汉诺塔问题的移动步骤:
(a1)把A柱上上面的n-1个盘子移动至B柱;
(a2)把A柱上剩下的一个盘子移动至C柱;
(a3)把B柱上的n-1个盘子移动至C柱。
在这之中a2步是很好实现的,而a1步与a3步却不能直接实现。若想实现第a1步,就需要进行以下三个步骤:
(b1)把A柱上上面的n-2个盘子移动至C柱;
(b2)把A柱上上面的一个盘子移动至B柱;
(b3)把C柱上的n-2个盘子移动至B柱。
这三步本质上和a1、a2、a3三步是相同的,只不过要移动的盘子少了一个,而目的地也从C柱变成了B柱。若想实现第b1步,就还需要进行三个步骤……
这种逆推的思想使得问题变为了一个个循环的过程,每一次过程都比原过程的盘子数少一个,循环往复,直到新过程中的盘子数变为1为止。这便是一个典型的递归方法。
借助C语言允许在函数中直接调用此函数本身的特性,我用C语言实现了汉诺塔问题的递归调用:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47//Hanoi.c
int step = 0;
void hanoi (int d, char first, char second, char third);
void out (char from, char to); //输出
int main(void)
{
int disk; //盘子数
char ch;
printf("Please input the number of diskes:");
scanf("%d", &disk);
printf("\n\nThis is the step to move %d diskes:\n", disk);
hanoi (disk, 'A', 'B', 'C');
printf("\nThis is all of %d steps.\n", step);
while ((ch = getchar()) != '\n') //按任意键继续
continue;
getchar();
return 0;
}
void hanoi (int n, char first, char second, char third)
{
if (n == 1)
{
out (first, third);
step++;
}
else
{
hanoi (n - 1, first, third, second);
out (first, third);
step++;
hanoi (n - 1, second, first, third);
}
}
void out (char from, char to)
{
printf("%c ---> %c\n", from, to);
}
程序实现了对用户指定盘子数n的移动步骤与总步数的输出,在MinGW编译环境下编译,运行效果如图6(输入3)。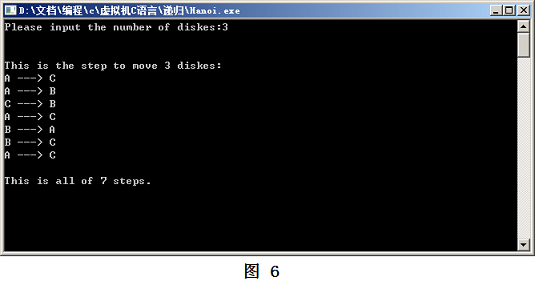
至此,关于汉诺塔问题的探究便告一段落。
第三部分、结论与启示
从最初的尝试,到大胆猜想,再到获得思路,最后成功把理论应用至实践,用计算机实现了对于n个盘子汉诺塔问题步骤的输出。整个探究过程帮助我透彻地理解了汉诺塔等递归问题的本质。其实递归问题不仅仅只有汉诺塔问题,例如“有5个人,问第5个人多少岁,他说比第4个人大两岁;问第4个人多少岁,他说比第3个人大两岁;问第3个人多少岁,他说比第2个人大两岁;问第2个人多少岁,他说比第1个人大两岁;最后问第1个人多少岁,他说是十岁。求第5个人多少岁。”这个问题就可以用递归方法来解决:第n个人的年龄用式子表达就是age(n)=age(n-1)+2(n>1), 10(n=1) 。
综合整篇文章,得出了S=2^n-1的结论以及n个盘子的解法,更重要的是成功应用了递归的思想,我从中体验到了一种数学的和谐之美,我们要发现生活中的数学之美,感受数学的魅力。